You can not select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
|
|
4 years ago | |
|---|---|---|
| Diff-Circle.avi | 4 years ago | |
| Readme.md | 4 years ago | |
| ficks.ipynb | 4 years ago | |
| output_2_0.png | 4 years ago | |
| output_5_0.png | 4 years ago | |
| output_5_7.png | 4 years ago | |
| output_5_48.png | 4 years ago | |
Readme.md
from fenics import *
from dolfin import *
import mshr
import matplotlib.pyplot as plt
import numpy as np
T = 60*60*5 #final step
num_steps = 50
dt = T/num_steps #step size
#2 Create mesh and define function space
domain = mshr.Circle(Point(0.,0.),1.0,60)
mesh = mshr.generate_mesh(domain, 25)
V = FunctionSpace(mesh, 'Lagrange', 1) #Lagrange are triangular elements
plot(mesh)
plt.show()
#3 Defining boundary conditions (Dirichlet)
D = 1.4E-7 #cm^2/s
u_D = Constant(0.1)
def Dirichlet_boundary(x, on_boundary):
return on_boundary
bc = DirichletBC(V, Constant(1), Dirichlet_boundary)
#Defining initial values and variational problem
u_n = interpolate(u_D,V)
u = TrialFunction(V)
v = TestFunction(V)
f = Constant(0)
F = u*v*dx+D*dt*dot(grad(u), grad(v))*dx-(u_n+dt*f)*v*dx
a, L = lhs(F), rhs(F)
#Resolution on time steps
u = Function(V)
t = 0
vtkfile = File('sol/solution.pvd')
for n in range(num_steps):
#update current time
t += dt
u_D.t = t
#compute solution
solve(a==L, u, bc)
#vtkfile << (u,t)
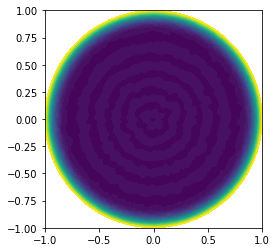
plot(u)
plt.show()
#update previous solution
u_n.assign(u)