25 changed files with 398 additions and 294 deletions
Unified View
Diff Options
-
+1 -0.gitignore
-
+0 -264.ipynb_checkpoints/main-checkpoint.ipynb
-
+206 -30main.ipynb
-
+191 -0main.md
-
BINoutput_1_0.png
-
BINoutput_4_1.png
-
BINoutput_4_10.png
-
BINoutput_4_11.png
-
BINoutput_4_12.png
-
BINoutput_4_13.png
-
BINoutput_4_14.png
-
BINoutput_4_15.png
-
BINoutput_4_16.png
-
BINoutput_4_17.png
-
BINoutput_4_18.png
-
BINoutput_4_19.png
-
BINoutput_4_2.png
-
BINoutput_4_20.png
-
BINoutput_4_3.png
-
BINoutput_4_4.png
-
BINoutput_4_5.png
-
BINoutput_4_6.png
-
BINoutput_4_7.png
-
BINoutput_4_8.png
-
BINoutput_4_9.png
+ 1
- 0
.gitignore
View File
| @ -0,0 +1 @@ | |||||
| .ipynb_checkpoints | |||||
+ 0
- 264
.ipynb_checkpoints/main-checkpoint.ipynb
File diff suppressed because it is too large
View File
+ 206
- 30
main.ipynb
File diff suppressed because it is too large
View File
+ 191
- 0
main.md
View File
| @ -0,0 +1,191 @@ | |||||
| ```python | |||||
| #1 Loading functions and modules | |||||
| from fenics import * | |||||
| import matplotlib.pyplot as plt | |||||
| T = 2.0 | |||||
| num_steps = 20 | |||||
| dt = T/num_steps | |||||
| rho = 7500 | |||||
| Cp = 500 | |||||
| k = 50 | |||||
| alpha = k/(rho*Cp) | |||||
| ``` | |||||
| ```python | |||||
| #2 Create mesh and define function space | |||||
| nx = 0.008 | |||||
| ny = 0.003 | |||||
| mesh = RectangleMesh(Point(0,0),Point(nx,ny),30, 30,'left') | |||||
| V = FunctionSpace(mesh, 'Lagrange', 1) #Lagrange are triangular elements | |||||
| plot(mesh) | |||||
| plt.show() | |||||
| ``` | |||||
|  | |||||
| ```python | |||||
| # Boundary conditions | |||||
| u0 = Constant(100) | |||||
| def boundary(x, on_boundary): | |||||
| return on_boundary | |||||
| bc = DirichletBC(V,u0, boundary) | |||||
| ``` | |||||
| ```python | |||||
| u_n = project(1, V) | |||||
| u = TrialFunction(V) | |||||
| v = TestFunction(V) | |||||
| f = Constant(0.0) | |||||
| F = u*v*dx + alpha*dt*dot(grad(u), grad(v))*dx-u_n*v*dx | |||||
| a, L = lhs(F), rhs(F) | |||||
| ``` | |||||
| Calling FFC just-in-time (JIT) compiler, this may take some time. | |||||
| ```python | |||||
| u = Function(V) | |||||
| t = 0 | |||||
| for n in range(num_steps): | |||||
| t += dt | |||||
| #u0.t = t | |||||
| solve(a == L, u, bc) | |||||
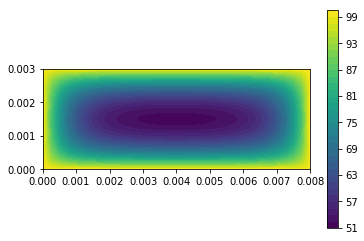
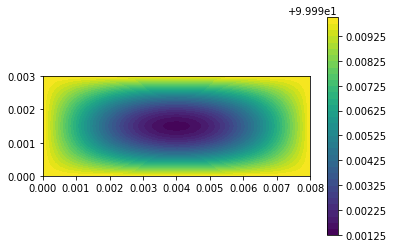
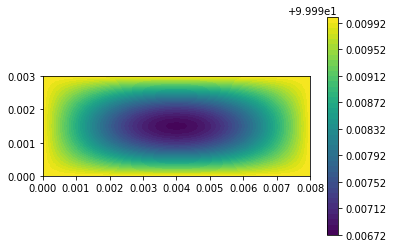
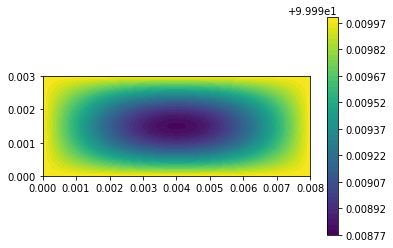
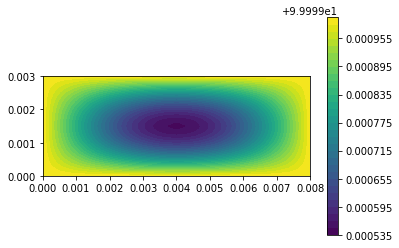
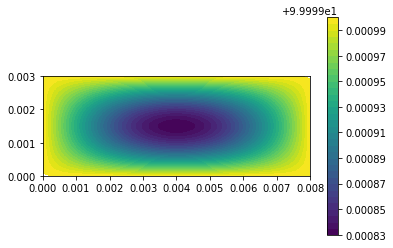
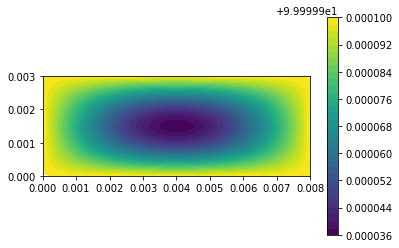
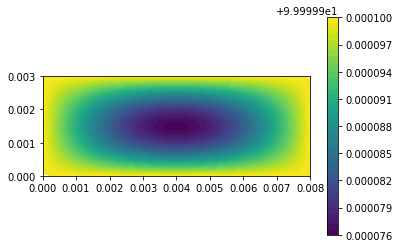
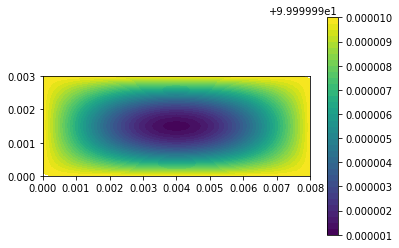
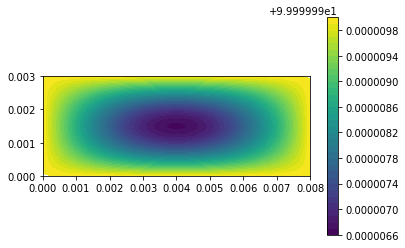
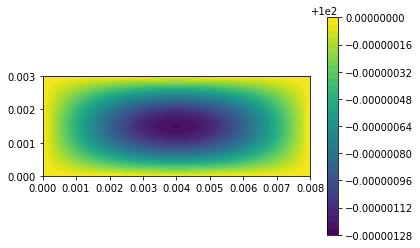
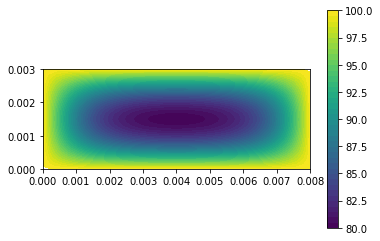
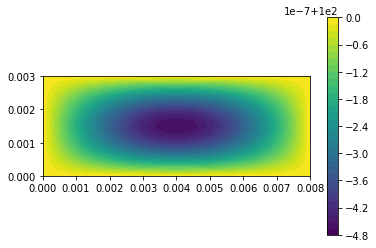
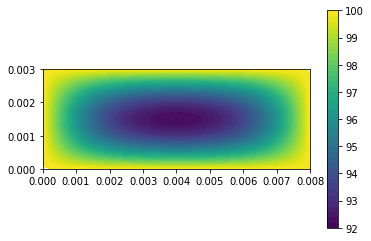
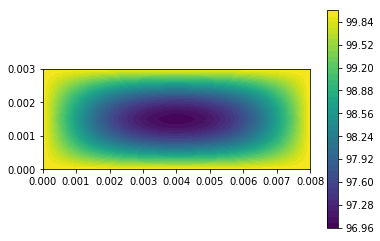
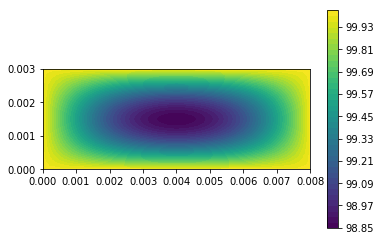
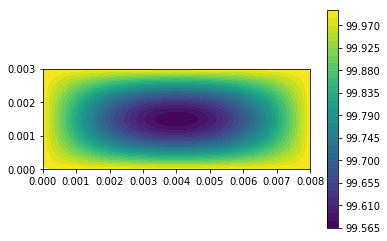
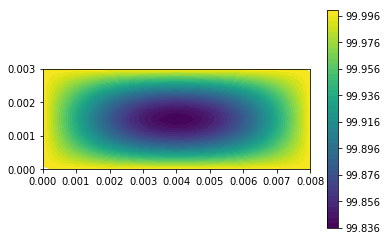
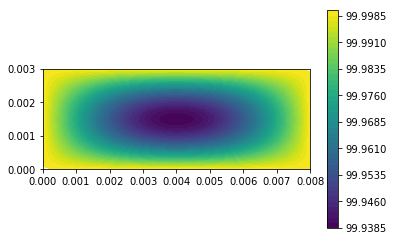
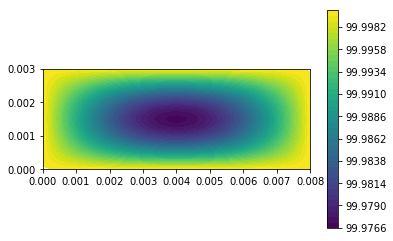
| c = plot(u,) | |||||
| plt.colorbar(c) | |||||
| plt.show() | |||||
| u_n.assign(u) | |||||
| ``` | |||||
| Calling FFC just-in-time (JIT) compiler, this may take some time. | |||||
|  | |||||
|  | |||||
|  | |||||
|  | |||||
|  | |||||
|  | |||||
|  | |||||
|  | |||||
|  | |||||
|  | |||||
|  | |||||
|  | |||||
|  | |||||
|  | |||||
|  | |||||
|  | |||||
|  | |||||
|  | |||||
|  | |||||
|  | |||||
| ```python | |||||
| 1E-7 | |||||
| ``` | |||||
| 1e-07 | |||||
| ```python | |||||
| 1e2 | |||||
| ``` | |||||
| 100.0 | |||||
| ```python | |||||
| 1E-7+1e2 | |||||
| ``` | |||||
| 100.0000001 | |||||
| ```python | |||||
| ``` | |||||