commit
5aada84c7c
9 changed files with 327 additions and 0 deletions
Unified View
Diff Options
-
+1 -0.gitignore
-
+219 -0Poisson.ipynb
-
+101 -0Readme.md
-
BINoutput_6_0.png
-
BINoutput_8_0.png
-
BINparaview-results.png
-
BINphysicalproblem.PNG
-
BINresulteq.png
-
+6 -0solution.pvd
+ 1
- 0
.gitignore
View File
| @ -0,0 +1 @@ | |||||
| .ipynb_checkpoints | |||||
+ 219
- 0
Poisson.ipynb
File diff suppressed because it is too large
View File
+ 101
- 0
Readme.md
View File
| @ -0,0 +1,101 @@ | |||||
| # Introduction | |||||
| The Poisson's equation is a second-order partial differential equation that stats the negative Laplacian $-\Delta u$ of an unknown field $u=u(x)$ is equal to a given function $f=f(x)$ on a domain $\Omega \subset \mathbb{R}^d$, most probably defined by a set of boundary conditions for the solution $u$ on the boundary $\partial \Omega$ of $\Omega$: | |||||
| $$-\Delta u =f \quad \text{in } \Omega\text{,}$$ | |||||
| $$u=u_0 \quad \text{on } \Gamma_D \subset \partial\Omega \text{,}$$ | |||||
| here the Dirichlet's boundary condition $u=u_0$ signifies a prescribed values for the unknown $u$ on the boundary. | |||||
| The Poisson's equation is the simplest model for gravity, electromagnetism, heat transfer, among others. | |||||
| The specific case of $f=0$ and a negative $k$ value, leaves to the Fourier's Law. | |||||
| ## Comparative analysis | |||||
| Along this example, the fenics platfomr is used to compare results obtained by solving the heat equation (Laplace equation) in 2-D: | |||||
| $$\frac{\partial^2 T}{\partial x^2}+ \frac{\partial^2 T}{\partial y^2}=0$$ | |||||
| the problem is defined by the next geometry considerations: | |||||
|  | |||||
| The resulting contour of temperature, solving using finite diferences, is shown next: | |||||
|  | |||||
| # Solving by Finite Element Method with Varational Problem formulation | |||||
| ```python | |||||
| #1 Loading functions and modules | |||||
| from fenics import * | |||||
| import matplotlib.pyplot as plt | |||||
| ``` | |||||
| ```python | |||||
| #2 Create mesh and define function space | |||||
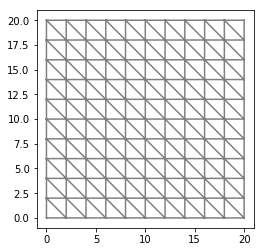
| mesh = RectangleMesh(Point(0,0),Point(20,20),10, 10,'left') | |||||
| V = FunctionSpace(mesh, 'Lagrange', 1) #Lagrange are triangular elements | |||||
| plot(mesh) | |||||
| plt.show() | |||||
| ``` | |||||
|  | |||||
| ```python | |||||
| #3 Defining boundary conditions (Dirichlet) | |||||
| tol = 1E-14 # tolerance for coordinate comparisons | |||||
| #at y=20 | |||||
| def Dirichlet_boundary1(x, on_boundary): | |||||
| return on_boundary and abs(x[1] - 20) < tol | |||||
| #at y=0 | |||||
| def Dirichlet_boundary0(x, on_boundary): | |||||
| return on_boundary and abs(x[1] - 0) < tol | |||||
| #at x=0 | |||||
| def Dirichlet_boundarx0(x, on_boundary): | |||||
| return on_boundary and abs(x[0] - 0) < tol | |||||
| #at x=20 | |||||
| def Dirichlet_boundarx1(x, on_boundary): | |||||
| return on_boundary and abs(x[0] - 20) < tol | |||||
| bc0 = DirichletBC(V, Constant(0), Dirichlet_boundary0) | |||||
| bc1 = DirichletBC(V, Constant(100), Dirichlet_boundary1) #100C | |||||
| bc2 = DirichletBC(V, Constant(0), Dirichlet_boundarx0) | |||||
| bc3 = DirichletBC(V, Constant(0), Dirichlet_boundarx1) | |||||
| bcs = [bc0,bc1, bc2,bc3] | |||||
| ``` | |||||
| ```python | |||||
| #4 Defining variational problem and its solution | |||||
| k =1 | |||||
| u = TrialFunction(V) | |||||
| v = TestFunction(V) | |||||
| f = Constant(0) | |||||
| a = dot(k*grad(u), grad(v))*dx | |||||
| L = f*v*dx | |||||
| # Compute solution | |||||
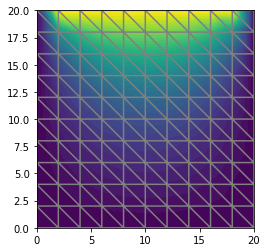
| u = Function(V) | |||||
| solve(a == L, u, bcs) | |||||
| # Plot solution and mesh | |||||
| plot(u) | |||||
| plot(mesh) | |||||
| # Save solution to file in VTK format | |||||
| vtkfile = File('solution.pvd') | |||||
| vtkfile << u | |||||
| ``` | |||||
|  | |||||
| # Results after editing color-map on paraview | |||||
|  | |||||
BIN
output_6_0.png
View File
BIN
output_8_0.png
View File
BIN
paraview-results.png
View File
BIN
physicalproblem.PNG
View File
BIN
resulteq.png
View File
+ 6
- 0
solution.pvd
View File
| @ -0,0 +1,6 @@ | |||||
| <?xml version="1.0"?> | |||||
| <VTKFile type="Collection" version="0.1"> | |||||
| <Collection> | |||||
| <DataSet timestep="0" part="0" file="solution000000.vtu" /> | |||||
| </Collection> | |||||
| </VTKFile> | |||||