commit
5aada84c7c
9 changed files with 327 additions and 0 deletions
+ 1
- 0
.gitignore
View File
+ 219
- 0
Poisson.ipynb
File diff suppressed because it is too large
View File
+ 101
- 0
Readme.md
View File
BIN
output_6_0.png
View File
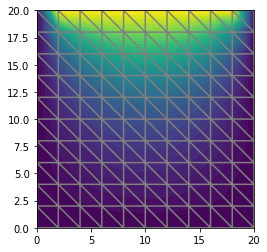
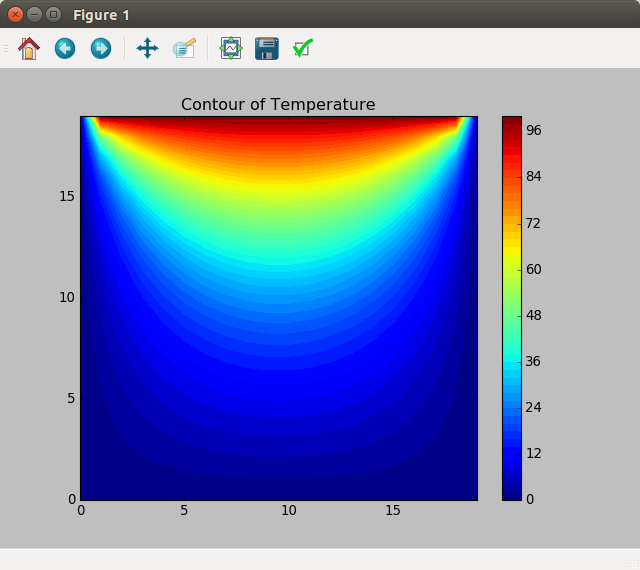
BIN
output_8_0.png
View File
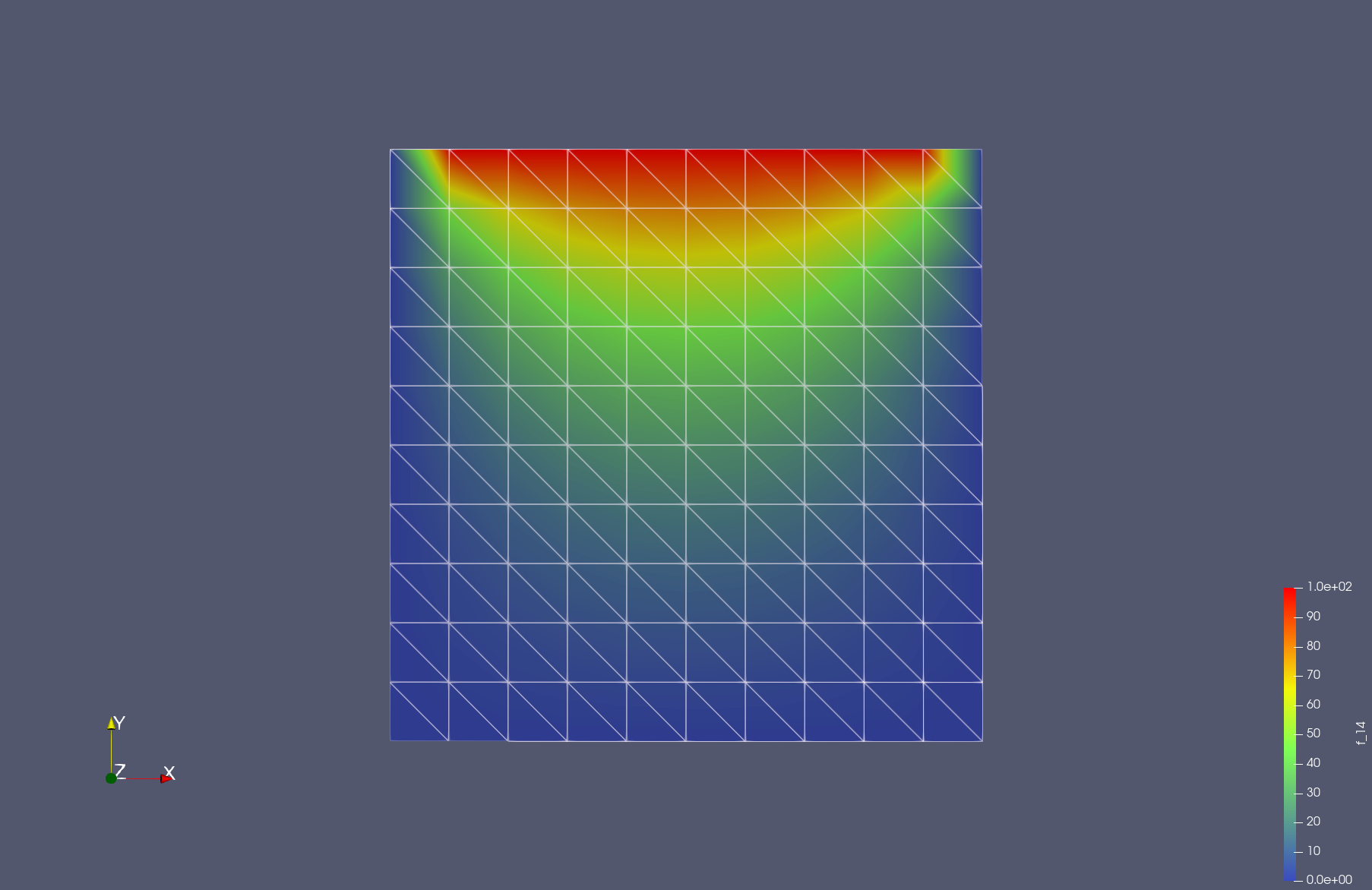
BIN
paraview-results.png
View File
BIN
physicalproblem.PNG
View File
BIN
resulteq.png
View File
+ 6
- 0
solution.pvd
View File
Loading…