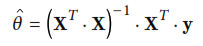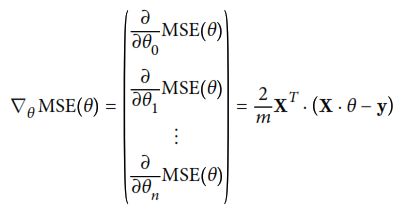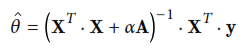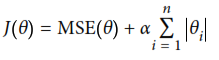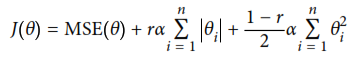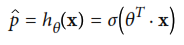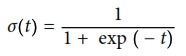|
|
5 years ago | |
|---|---|---|
| fig | 5 years ago | |
| Batchgradientdecent.py | 5 years ago | |
| Descensogradientecomp.py | 5 years ago | |
| Earlystop.py | 5 years ago | |
| README.md | 5 years ago | |
| RegresionElastic.py | 5 years ago | |
| RegresionLasso.py | 5 years ago | |
| RegresionRidge.py | 5 years ago | |
| Regresionlinealmatricial.py | 5 years ago | |
| regresionpolinomial.py | 5 years ago | |
| stochasticgradientdescent.py | 5 years ago | |
README.md
Python machine learning
This repository has example codes about the reading found on Chapter 4 "Training models" from the book Hands-On Machine Learning with Scikit-Learn and TensorFlow by Aurélien Géron
Usage
Codes are written on python and can be executed by both python 2 and 3 as long as the libraries are available.
Report
Siguiendo el orden que se encuentra en el libro, Comenzamos con el analisis de regresión lineal que utiliza la función de costo mostrada en la siguiente figura:
Se utilizan como datos originales para las funciones lineales la ecuación: 4 + 3 * X agregandole un error con distribución normal. El primer ejemplo "Regresionlinealmatricial.py", entrega el resultado mostrado a continuación:
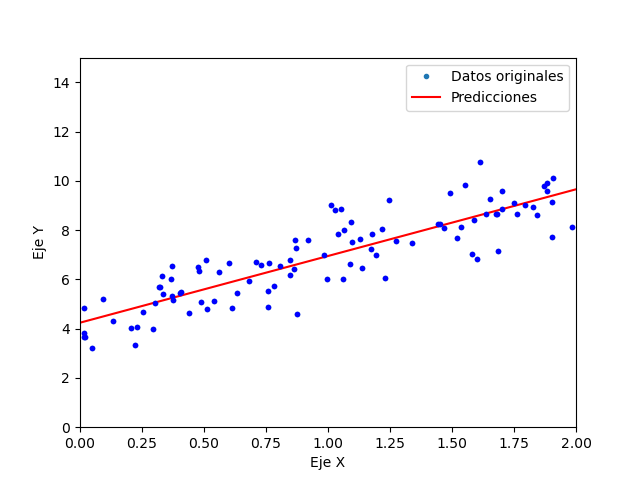
Llegando la regresión a la ecuación 3.96263358 + 3.02663111 * X siendo esta muy cercana a la original.
Ya que las operaciones matriciales necesarias para resolver una regresión lineal son en general muy lentas y complejas de computar, se muestra la opción de optimizar el algoritmo mendiante una opción más optima: descenso por gradiente. Este método utiliza el vector gradiente de la función de costo original, que se muestra a continuación:
Uno de los parámetros más importantes dentro del método de descenso por gradiente es el tamaño de los pasos que se dan entre cada descenso, ya que si es muy pequeño el algoritmo necesita muchas iteraciones para converger, mientras que si es muy alto, podría diverger al saltar el valle donde se encuentra el mínimo.
Para ilustrar lo anterior y como primero ejemplo, se muestra desde el código "Descensogradientecomp.py", el comportamiento obtenido al utilizar diferentes valores de paso "step":
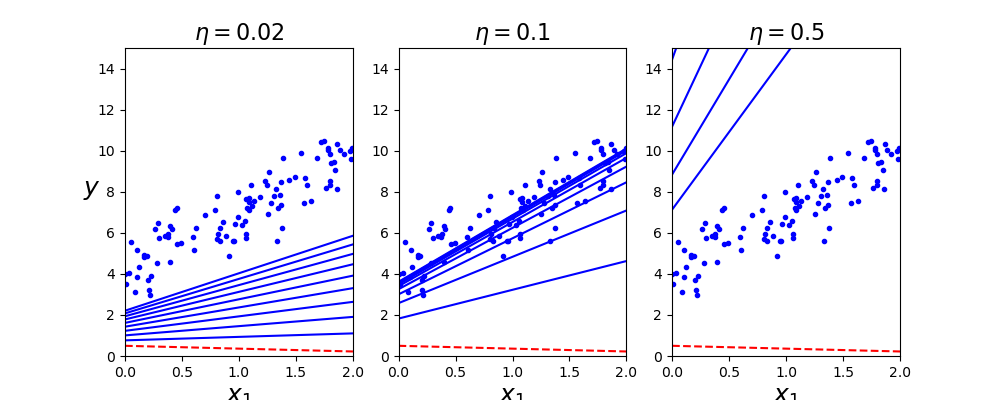 En la figura anterior se puede observar la aproximación a los datos, como se esperaba, el comportamiento para n muy pequeño provoca que se necesiten muchas iteraciones para alcanzar el resultado, en la segunda un acercamiento optimo, mientras que en la tercera opción, un crecimiento demasiado grande resultando en sobrepaso.
En la figura anterior se puede observar la aproximación a los datos, como se esperaba, el comportamiento para n muy pequeño provoca que se necesiten muchas iteraciones para alcanzar el resultado, en la segunda un acercamiento optimo, mientras que en la tercera opción, un crecimiento demasiado grande resultando en sobrepaso.
A continuación, se presenta un metódo optimizado de descenso por gradiente, ya que el anterior utiliza todo el conjunto de datos para computar su resultado, se vuelve lento de ejecutar, como una primera alternativa, se presenta el descenso por gradiente estocástico que en lugar de tomar todo el arreglo, toma aleatoriamente una muestra de los datos a la vez en múltiples ocasiones, lo que le permite utilizar menos memoria por iteración volviendose más fácil de ejecutar.
En el mismo código "Regresionlinealmatricial.py", en la siguiente sección, se encuentra un ejemplo de esta variación de descenso por gradiente, el resultado se muestra a continuación.
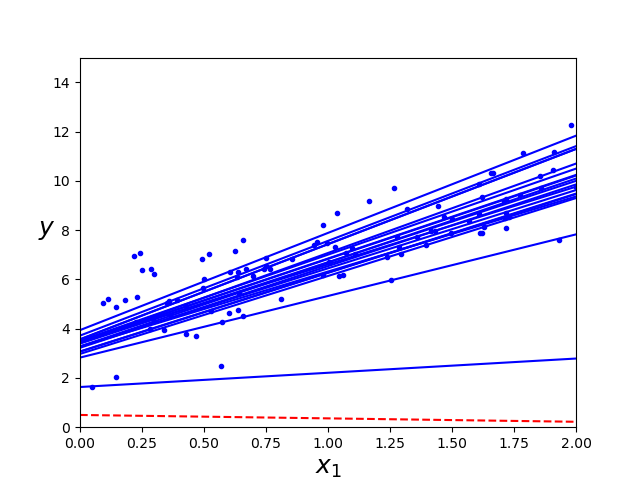
El último ejemplo de descenso por gradiente, es una combinación de los dos anteriores, descenso por gradiente por mini lotes, en lugar de iterar a través de todo el arreglo de datos o de sólo un punto, se itera sobre subconjuntos de los datos lo que otorga ventajas en cuestiones de optimización matricial. En la última sección del código, se encuentra esta implementación y la comparación entre los 3 metódos, se muestra a continuación.
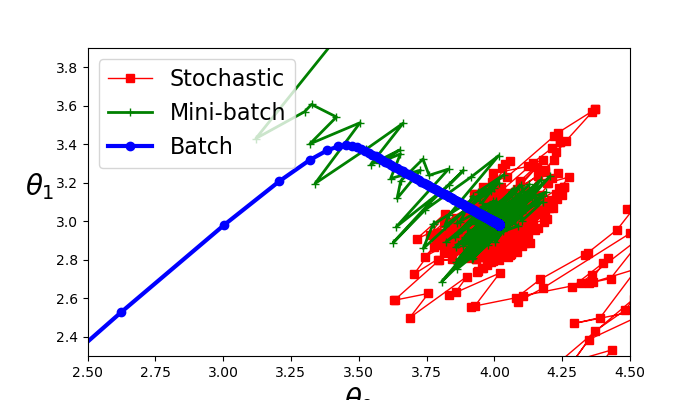
En la figura se puede apreciar que todos los metódos se aproximan a los valores originales de la ecuación; 4 y 3. El metodo de lote, tiene el comportamiento más estable mientras que los otros dos oscilan entre sus cambios de valores hasta establecerse en un punto.
Para casos en que los datos a analizar, no puedan ser aproximados por una linea recta, se muestran metódos alternos de solución, comenzando por la regresión polinómica. Este metódo utiliza la misma metodología que la regresión lineal con la diferencia que agrega potencias extras según el grado del polinomio a cada caracteristica. Para los siguientes polinomios, la ecuación que origina los datos es: 0.5 * X^2 + X + 2 agregando nuevamente ruido aleatorio a los datos. Los resultados obtenidos con la regresión polinomica que se encuentra en el código "regresionpolinomial.py" se muestran a continuación
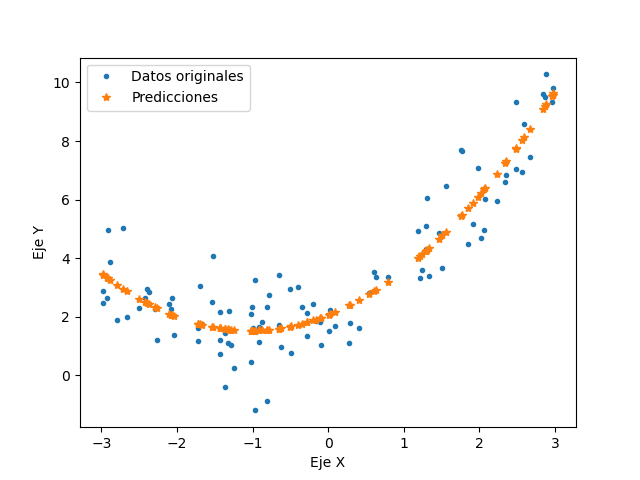
De esta regresión se obtiene una aproximación con un 85.17% de exactitud, llegando a los valores 0.43536028X^2 + 1.01274982X + 2.15068581 que son muy próximos a los valores originales.
En el texto se menciona que uno de los principales problemas de estas regresiones lineales, son los riesgos de sobreestimación y subestimación. Así como hay metódos para detectar estos dos problemas, como lo es la validación cruzada y observar el comportamiento entre el entrenamiento y la validación, se ofrecen tres modelos lineales regularizados.
El primero de estos modelos es Ridge Regression que agrega un termino a la función de costo que forza el algoritmo de aprendizaje para no sólo encajar con los datos si no también mantener los pesos del modelo tan pequeños como sea posible. La ecuación utilizada por este metódo es la siguiente
El código "RegresionRidge.py" se utiliza para aplicar esta regresión, obteniendo un porcentaje de exactitud máximo de 85.62% y llegando a los valores 0.47997248X^2 + 0.99088271X + 2.06616787
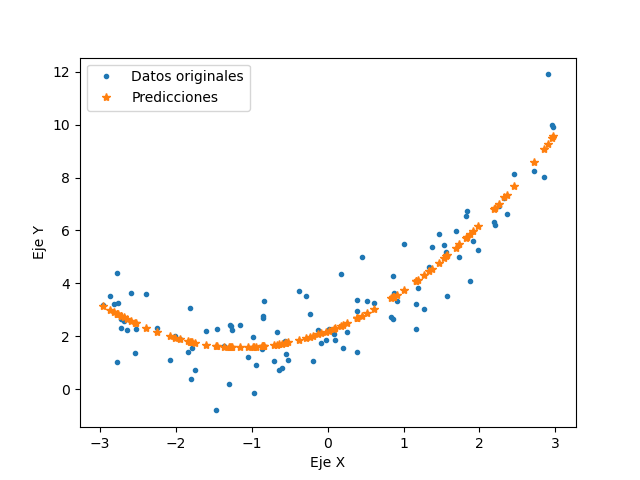
El segundo de estos modelos es Lasso Regression que igual que el termino anterior, utiliza un termino agregado a la función de costo pero con una norma diferente, como se muestra a continuación
El código "RegresionLasso.py" es el que se utiliza para este ejemplo, el modelo obtuvo una exactitud máxima del 85.39%, teniendo el valor de 0.4544238X^2 + 0.98603098X + 2.15597262. El resultado obtenido se muestra a continuación.
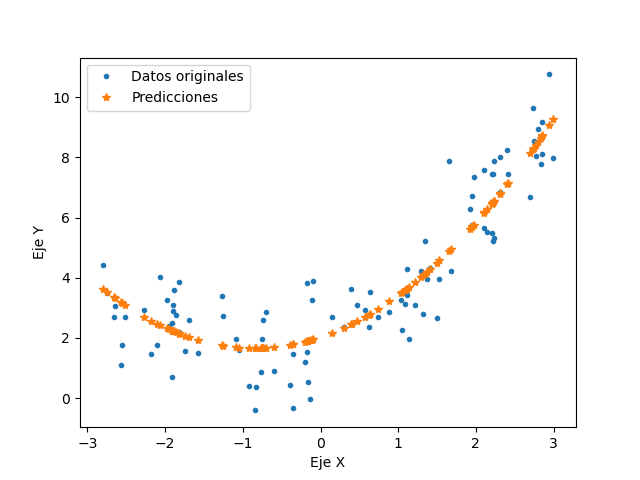
Por último, se presenta el modelo de red elastica, esta se encuentra en un punto medio entre la regresión Ridge y Lasso, ya que el término de regularización es una combinación entre los otros dos términos. Esta combinación se puede controlar con el valor del factor r, cuando vale 0, el comportamiento se asemeja a Ridge, mientras que al valer 1, es equivalente a Lasso. La función de costo se muestra a continuación
El código "RegresionElastic.py" es el que se utiliza para este último ejemplo, se encontró una exactitud máxima del 87.72% al utilizar este método y se llegó a los valores 0.47876133X^2 + 1.00204149X+ 2.14224417, la grafica resultante se encuentra a continuación
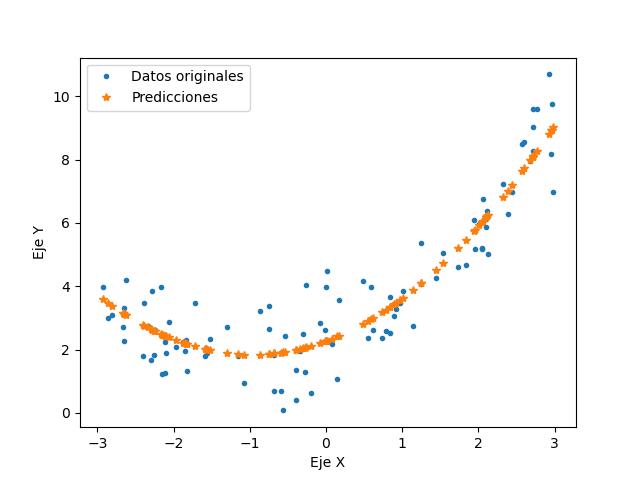
El tema final del capitulo, es la regresión logistica. Este tipo de regresión es comunmente utilizada para estimar la probabilidad de que una instancia pertenezca a una clase en particular, si la probabilidad estimada es mayor que 50% entonces, el modelo predice que la instancia pertenece a la clase 1, en caso contrario, pertenece a la clase 0, en pocas palabras, es un clasificador binario. Este clasificador utiliza la siguiente ecuación
Al igual que un modelo de regresión lineal, la regresión logistica computa una suma potenciada de las caracteristicas de entrada pero en lugar de sacar el resultado directamente, saca la logistica de este resultado, con la ecuación anterior. La logistica la hacen computando la función sigmoide que se muestra a continuación, esta función saca un numero entre 0 y 1.