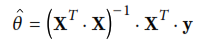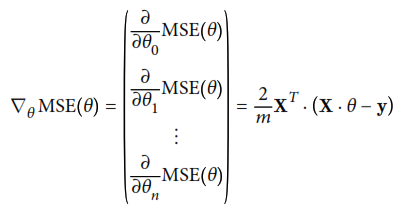|
|
5 years ago | |
|---|---|---|
| fig | 5 years ago | |
| Batchgradientdecent.py | 5 years ago | |
| Descensogradientecomp.py | 5 years ago | |
| Earlystop.py | 5 years ago | |
| README.md | 5 years ago | |
| RegresionElastic.py | 5 years ago | |
| RegresionLasso.py | 5 years ago | |
| RegresionRidge.py | 5 years ago | |
| Regresionlinealmatricial.py | 5 years ago | |
| regresionpolinomial.py | 5 years ago | |
| stochasticgradientdescent.py | 5 years ago | |
README.md
Python machine learning
This repository has example codes about the reading found on Chapter 4 "Training models" from the book Hands-On Machine Learning with Scikit-Learn and TensorFlow by Aurélien Géron
Usage
Codes are written on python and can be executed by both python 2 and 3 as long as the libraries are available.
Report
Siguiendo el orden que se encuentra en el libro mencionado, Comenzamos con el analisis de regresión lineal que utiliza la función de costo mostrada en la siguiente figura:
Esta ecuación implementada en el código Regresionlinealmatricial.py, se utilizan como datos originales para las funciones lineales, la ecuación: 4 + 3 * X agregandole un error con distribución normal.
El primer ejemplo, entrega el resultado mostrado a continuación:
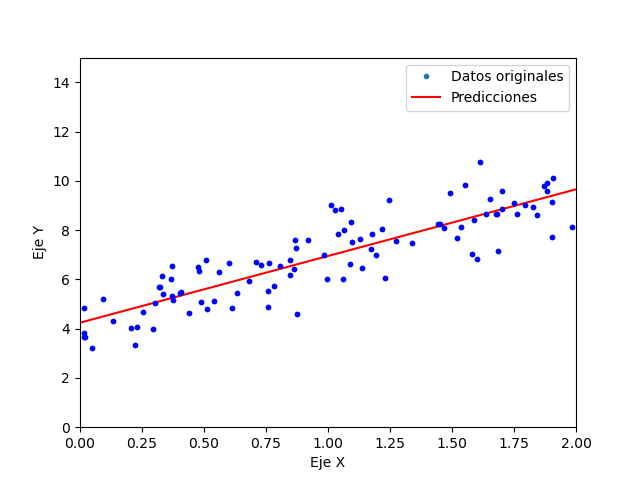
Llegando la regresión a la ecuación 3.96263358 + 3.02663111 * X siendo esta muy cercana a la original.
Ya que las operaciones matriciales necesarias para resolver una regresión lineal son en general muy lentas y complejas de computar, se muestra la opción de optimizar el algoritmo mendiante una opción más optima: Descenso por gradiente. Este método utiliza el vector gradiente de la función de costo original, que se muestra a continuación:
Uno de los más importantes parámetros dentro del método de descenso por gradiente es el tamaño de los pasos que se dan entre cada descenso, ya que si es muy pequeño el algoritmo necesita muchas iteraciones para converger, mientras que si es muy alto, podría diverger al saltar el valle donde se encuentra el mínimo.